Lesson 19: Drawing a double-helix

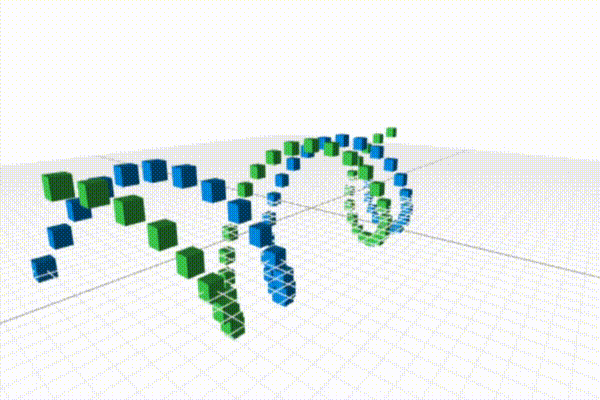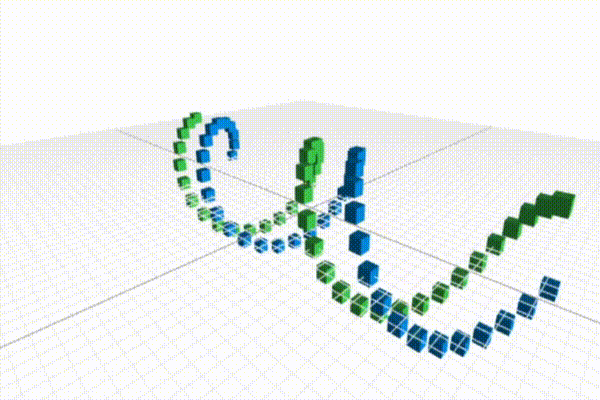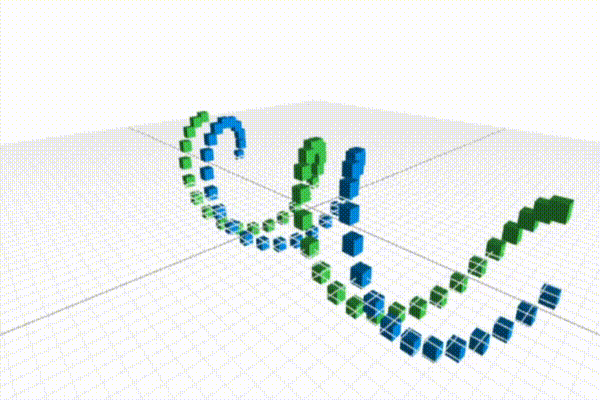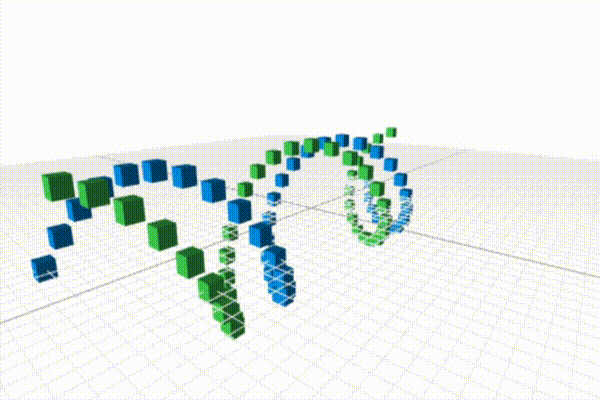
double helix demo

The previous lesson demonstrated that a small modification to the original ring code could produce a helix. In this lesson, we're going to modify our original helix, to create a double-helix as shown above. Let's start with the code for creating a single-helix:

Hold shift + scroll to zoom

1
2
3
4
5
6
7
8
9
10
11
12
import math
from ctb import place
RADIUS = 5
SEGMENTS = 20
for position in range(2 * SEGMENTS):
  radians = 2 * math.pi * position / SEGMENTS
  x = RADIUS * math.cos(radians)
  y = RADIUS * math.sin(radians)
  z = position - SEGMENTS
  place(x, y, z)
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

At the end of the lesson, I challenged you to add another helix to the mix and create what's known as a double-helix. To add another helix to the mix, we need to make sure the helixes don't interfere with each other. We can make them run side-by-side if we offset one compared to the other. A good way to do so is to add a constant amount to the radians variable. Since a full circle is 2π, let's set the offset to be one-quarter of a circle, or π/2.

Hold shift + scroll to zoom

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import math
from ctb import place, Color
RADIUS = 5
SEGMENTS = 20
for position in range(2 * SEGMENTS):
  radians1 = 2 * math.pi * position / SEGMENTS
  x = RADIUS * math.cos(radians1)
  y = RADIUS * math.sin(radians1)
  radians2 = radians1 + (math.pi / 2)
  x2 = RADIUS * math.cos(radians2)
  y2 = RADIUS * math.sin(radians2)
  z = position - SEGMENTS
  place(x, y, z, Color.BLUE)
  place(x2, y2, z, Color.GREEN)
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

Note that I've split the code into multiple paragraphs: one for the calculations of the first helix, one for the second, a short one to figure out common components (the z coordinate), and a final one to place the cubes.

You'll notice that we're starting to repeat ourselves in this piece of code. And as we discussed, keeping code DRY (Don't repeat yourself) is a good idea. In the next lesson, I'll go over functions and we'll use them as a mechanism to reduce repetition in this code and make it much more readable.

For now, your exercise is to go even further with the helixes. Try creating a triple-helix. How about a quadruple-helix?