Lesson 15: Drawing a ring

Now that we know how loops work, we can try to create the following ring structure. In future lessons, we'll build on this and produce more complex and awesome structures.

A math refresher first

Before we get started, we need to learn a bit of math. If you're mathematically inclined, feel free to skip this section.

Calculating the x and y coordinates of any given point in a circle

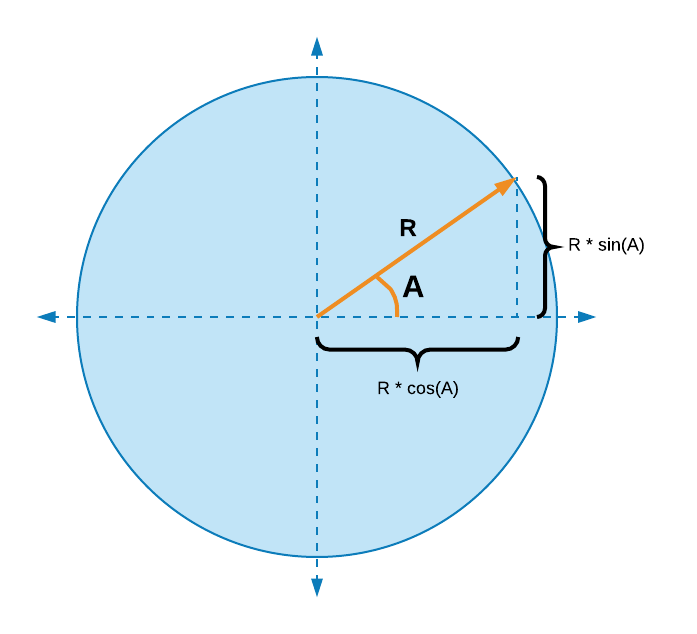
The diagram above illustrates how to calculate the x and y coordinates of the point where the orange line intersects the circle. If the angle between the orange line and the x axis is represented by A and the length of the orange line is R (short for Radius of the circle), then the x coordinate of that point is R * cos(A) and the y coordinate is R * sin(A).

Radians

One last thing you need to know about before we jump into the code: radians. Angles can be measured in either degrees or radians. As you may already know, a full circle is 360°. But a full circle can also be expressed in terms of radians as 2π, where π is approximately 3.1415.

For more details on both these concepts, check out this Khan Academy tutorial.

First attempt at a ring

With all the knowledge from the section above, we can create a simple ring:

Let's deconstruct this piece of code:

• Python has a lot of useful mathematical functions in its math module. Instead of importing them directly using from math import pi, cos, sin (which would also be a valid approach), we decided to import the entire math module and just use selective parts of the module using the math.pi syntax. This is a useful pattern and worth remembering.

• We set RADIUS and SEGMENTS as variables near the top of our code. Using ALL_CAPS to store common constant values is a popular pattern. It increases the readability of your code. It also makes it easy to modify the behavior of your code. Try changing the radius or the number of segments by adjusting those 2 variables and see how easily you can change your ring.

• We iterate over range(SEGMENTS), meaning that we iterate over the list [0, 1, 2, 3, ..., (SEGMENTS-1)]. Each of those numbers represents a cube in the ring. We call this index our position.

• For each position index, we calculate the number of radians from the x axis. Think of the diagram above for this. The whole circle is 2π radians. So the angle (in radians) of our point on the circle (corresponding to the position) is the fraction position/SEGMENTS of 2π. That makes it 2π * (position/SEGMENTS). In Python, the value of the constant π can be found in math.pi.

• The value of the x coordinate is RADIUS * math.cos(radians) and the value of the y coordinate is RADIUS * math.sin(radians). This has been explained in the previous section.

• And once we have the x and y coordinates, we can go ahead and place the cube using place(x, y, 0). We don't need to change the z coordinate to make a simple ring.

In the next lesson, we'll try to color this ring and in the process learn about the modulo operator.